# The Power of NumPy

## What is NumPy?

[NumPy](https://numpy.org/) is a numerical library written in Python that focuses on matrix objects called `ndarrays`. NumPy delegates most of its core computation to underlying C and Fortran code, which means that NumPy is very fast. Indeed, many people use Python for financial research because of the functionality provided by NumPy.

## Relationship to Pandas

Let's look back at our DataFrame `df`.

![](https://assets.omscs.io/notes/D38A6927-FF9C-4865-83D8-32FED6A19B63.png)

Just as NumPy is a wrapper around C and Fortran code, pandas is a wrapper of sorts around NumPy.

![](https://assets.omscs.io/notes/37569F60-C8EC-4B64-A5C3-EE1F2AD9B8C0.png)

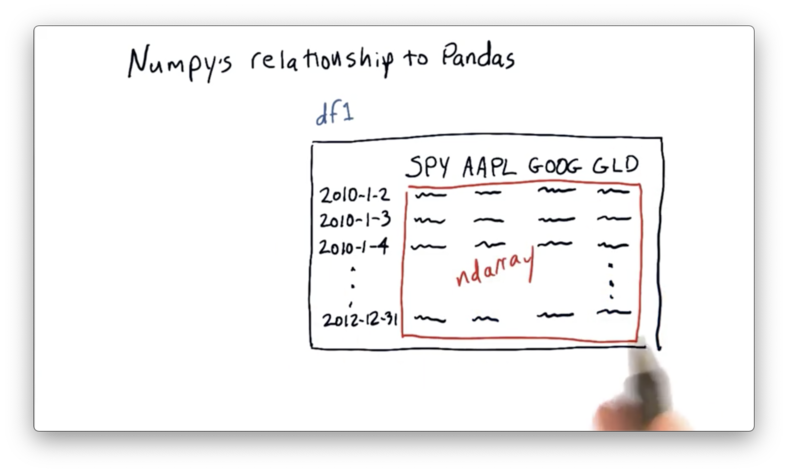
As the picture above illustrates, pandas builds `df` on top of an ndarray. We can retrieve the internal ndarray directly from a DataFrame `df` with the following code:

```python
df.values
```

We don't have to do this explicitly, though; in fact, we can interact with `df` as though it were the underlying ndarray. In other words, functionality that is available to the internal ndarray is available to `df`.

Of course, we create DataFrames because pandas builds a lot of great functionality on top of these ndarrays. For example, pandas provides expressive ways to access data in the array, such as symbol-based column indexing and date-based row indexing in the case of `df`.

### Documentation

* [pandas.DataFrame.values](https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.DataFrame.values.html)
* [pandas.DataFrame.to\_numpy](https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.DataFrame.to_numpy.html#pandas.DataFrame.to_numpy)

## Notes on Notation

Let's look at accessing information in an ndarray `nd`. The basic syntax for accessing information about a `row` and `col` looks like this:

```python
nd[row, col]
```

NumPy uses **zero-based indexing**, which means that we access the very first cell using `nd[0,0]`, not `nd[1,1]`.

To access the cell in the fourth row and the third column, for example, we do the following:

```python
nd[3, 2]
```

NumPy also supports *slicing*. Generally, to retrieve the cells bounded by the (zero-based) index values `start_row` , `end_row`, `start_col` and `end_col`, we do the following:

```python
nd[start_row:end_row + 1, start_col:end_col + 1]
```

Concretely, if we want to retrieve the cells in `nd` that are in the first three rows and second and third columns, we do the following:

```python
nd[0:3, 1:3]
```

Note that NumPy slicing is upper-bound exclusive, which is why we have to add one to the end of our ranges.

If we want to select all of the rows or all of the columns in `nd`, we can pass in the colon by itself, like this:

```python
nd[:, 1:3] # select all rows, second and third column
nd[0:2, :] # select first and second row, all columns
```

NumPy also provides syntax for **negative indexing**. Passing in a negative number in the slicing expression allows us to index from the "bottom" and/or "right" of `nd`. For example:

```python
nd[-1, :] # select last row, all columns
nd[:, -2] # select all rows, second-to-last column
nd[-2:, :] # select second-to-last and last row, all columns
nd[:, 0:-1] # select all rows, all columns except last
```

Note that negative indexing is *not* zero-based. The last row/column is referenced by -1, not -0.

### Documentation

* [Indexing](https://docs.scipy.org/doc/numpy/user/basics.indexing.html)

## Replace a Slice Quiz

![](https://assets.omscs.io/notes/1E2BC0CC-EADA-4431-ABDF-AE07857CF80D.png)

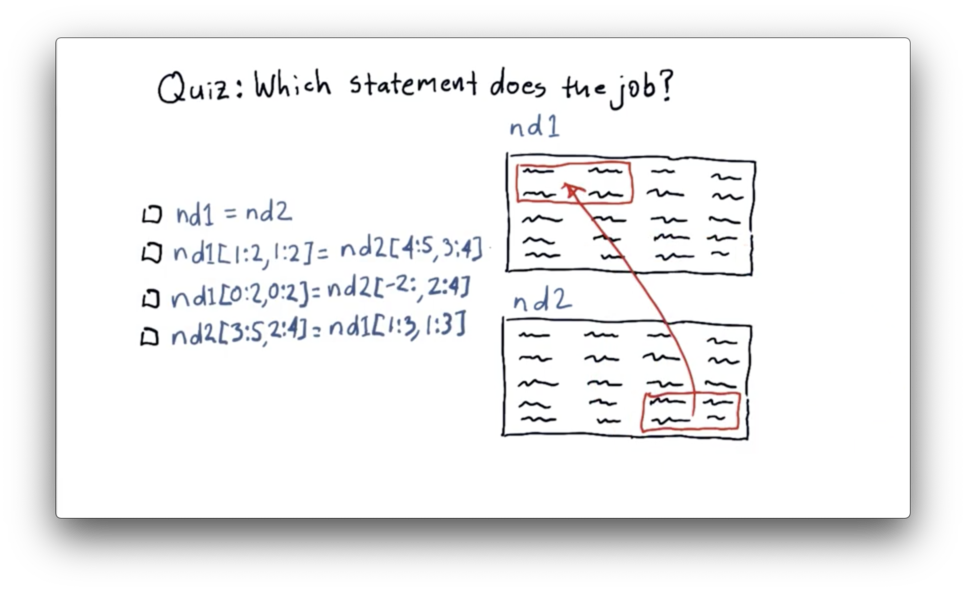
We need to move data from the last two rows and the last two columns of `nd2` to the first two rows and the first two columns of `nd1`.

## Replace a Slice Quiz Solution

![](https://assets.omscs.io/notes/60DEA1EE-99C0-4CC6-95F7-B01B9681CD59.png)

Let's first look at how we can slice `nd2` to extract the data we want. We can slice the last two rows using negative indexing: `-2:`. We can slice the last two columns as `2:4`. Remember that NumPy indexing is upper-bound exclusive.

Now let's see how we can transplant that data into `nd1`. We can select the first two rows of `nd1` as `0:2`, and we can select the first two columns as `0:2`.

The complete data transfer can be accomplished with the following code:

```python
nd1[0:2, 0:2] = nd2[-2:, 2:4]
```

### Documentation

* [Indexing](https://docs.scipy.org/doc/numpy/user/basics.indexing.html)

## Creating NumPy Arrays

As we said earlier, we can access the underlying NumPy array from a DataFrame through the `values` property. Alternatively, we can create a NumPy array from scratch:

```python
import numpy as np
nd = np.array([2, 3, 4])
```

If we print `nd` we see the following.

![](https://assets.omscs.io/notes/2354DAFA-F1C6-4C1F-8EAF-68361CEE0BE9.png)

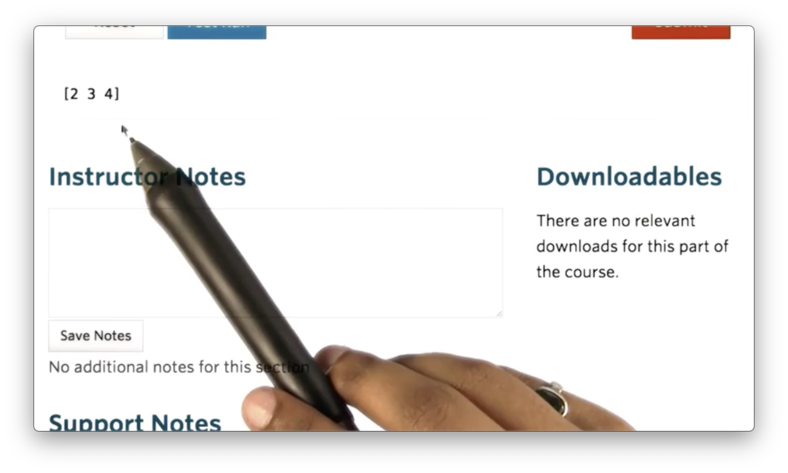
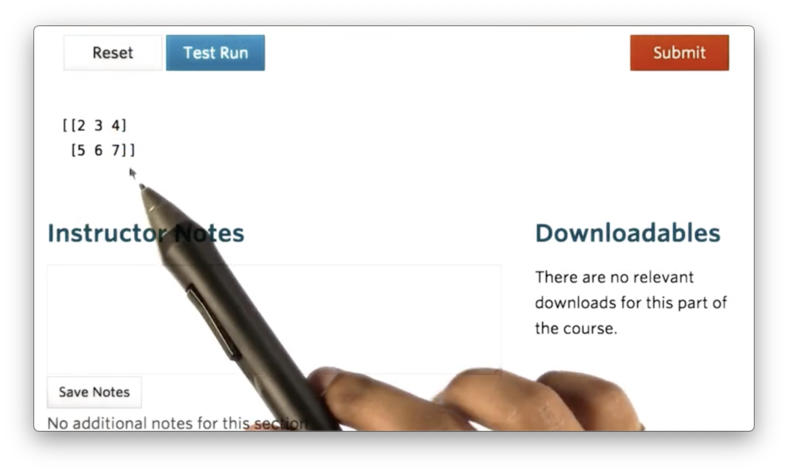
We can create a two-dimensional array by passing in a list of lists:

```python
nd = np.array([(2, 3, 4),(5, 6, 7)])
```

If we print `nd` we see the following.

![](https://assets.omscs.io/notes/D3EFFDD6-24C4-48CA-88FE-55FCC2E870F3.png)

### Documentation

* [numpy.array](https://docs.scipy.org/doc/numpy/reference/generated/numpy.array.html)

## Arrays with Initial Values

NumPy offers several functions for creating empty arrays with initial values. For certain computations, growing arrays incrementally can be a costly operation, so initializing empty arrays upfront may be more efficient.

We can create an empty array with shape `n` like so:

```python
np.empty(n)
```

For example, we can create an empty one-dimensional array with five elements, or an empty two-dimensional array with five rows and four columns like this:

```python
np.empty(5)
np.empty((5, 4))
```

We can even create a three-dimensional array with five rows, four columns, and a depth of three:

```python
np.empty((5, 4, 3))
```

If we print the two-dimensional array created by `np.empty((5, 4))`, we see the following.

![](https://assets.omscs.io/notes/29648C43-7BB5-47C7-99A7-79283F30C9B6.png)

Interestingly, the empty array is not actually empty; instead, the array is filled with whatever values are present in memory at the time of array creation. Note that all of the values in the empty array are floating-point numbers.

We can create an array full of ones with the `np.ones` function, and the following code shows how to create such an array with five rows and four columns:

```python
np.ones((5, 4))
```

Indeed, we see the following array when we print.

![](https://assets.omscs.io/notes/09666E20-37ED-4A8A-AB87-1E278D9487E3.png)

### Documentation

* [numpy.empty](https://docs.scipy.org/doc/numpy/reference/generated/numpy.empty.html)
* [numpy.ones](https://docs.scipy.org/doc/numpy/reference/generated/numpy.ones.html)

## Specify the Data Type Quiz

![](https://assets.omscs.io/notes/1A04EA50-3DE1-4BA2-85E6-B852F298AB7B.png)

We saw that the elements in an array created by `np.ones` are floats by default. Our task here is to update the call to `np.ones` and pass in a parameter that tells NumPy to give us integers instead of floats.

## Specify the Data Type Quiz Solution

![](https://assets.omscs.io/notes/29CA699E-4950-4B22-948D-A38910E9A9EA.png)

We can accomplish this change with the following code:

```python
np.ones((5, 4), dtype=np.int_)
```

### Documentation

* [numpy.ones](https://docs.scipy.org/doc/numpy/reference/generated/numpy.ones.html)
* [Data types](https://docs.scipy.org/doc/numpy/user/basics.types.html#data-types)

## Generating Random Numbers

NumPy also comes with a bunch of handy functions for generating ndarrays filled with random values. These functions are defined in NumPy's `random` module.

The `random` method on the `random` module allows us to generate an ndarray filled with random, uniformly sampled floating-point numbers in the range of 0.0 (inclusive) to 1.0 (exclusive).

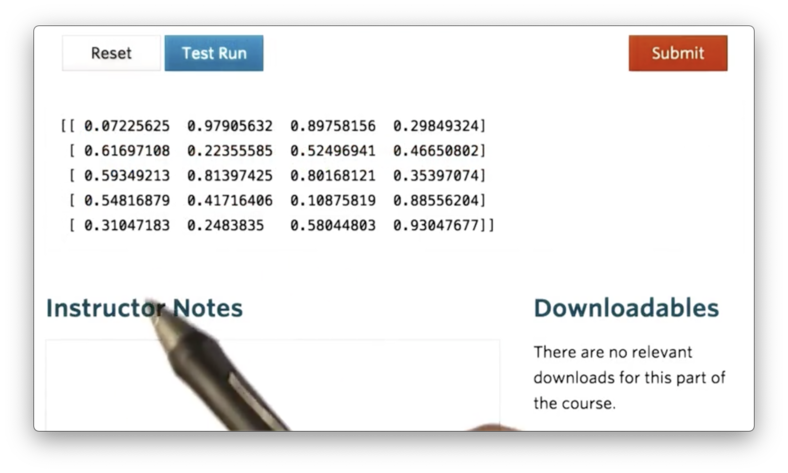
For example, we can generate such an ndarray with five rows and four columns using the following code:

```python
np.random.random((5,4))
```

If we print this ndarray, we see the following.

![](https://assets.omscs.io/notes/768AFDB2-5982-43F2-B150-6702C274B722.png)

A slight variant of the `random` method is the `rand` method, which, instead of accepting a tuple corresponding to the shape, accepts a sequence of numbers describing the dimensions of the ndarray.

We can generate the same ndarray as above with `rand` using the following code:

```python
np.random.rand(5, 4)
```

NumPy exposes this syntax because it matches the more established MatLab syntax. However, we should use the `random` method, as the shape tuple is a consistent construct seen across NumPy.

Both `rand` and `random` sample uniformly from the range `[0.0, 1.0)`. We can instead generate an ndarray with elements sampled from a **Gaussian** (normal) distribution, using the `normal` method.

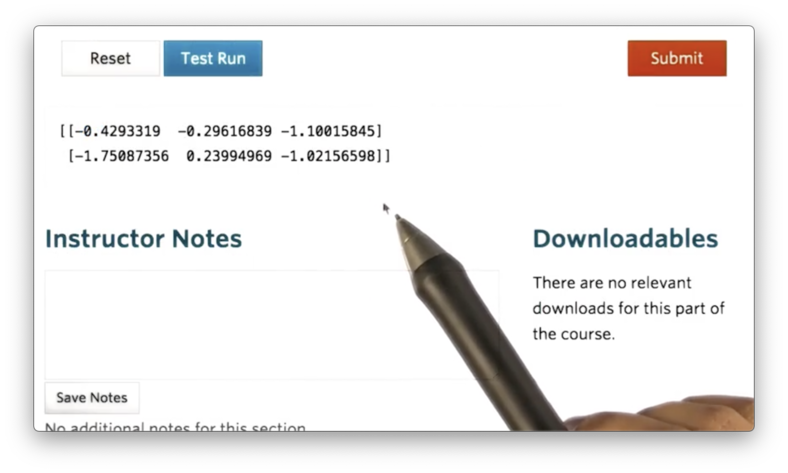
For instance, we can create such an ndarray with two rows and three columns like so:

```python
np.random.normal(size=(2,3))
```

If we print this ndarray, we see the following.

![](https://assets.omscs.io/notes/14C3149A-6447-4541-814C-CA099328CE48.png)

By default, the `normal` method samples from a Gaussian distribution with a mean of 0 and a standard deviation of 1. We can also sample from normal distributions parameterized by different means and standard deviations.

For example, we can generate an ndarray whose elements are sampled from a normal distribution with a mean of 50 and a standard deviation of 10 like this:

```python
np.random.normal(50, 10, size=(2,3))
```

If we print this ndarray, we see the following.

![](https://assets.omscs.io/notes/84B46E3D-1B72-4239-AD47-4F3A039FDA49.png)

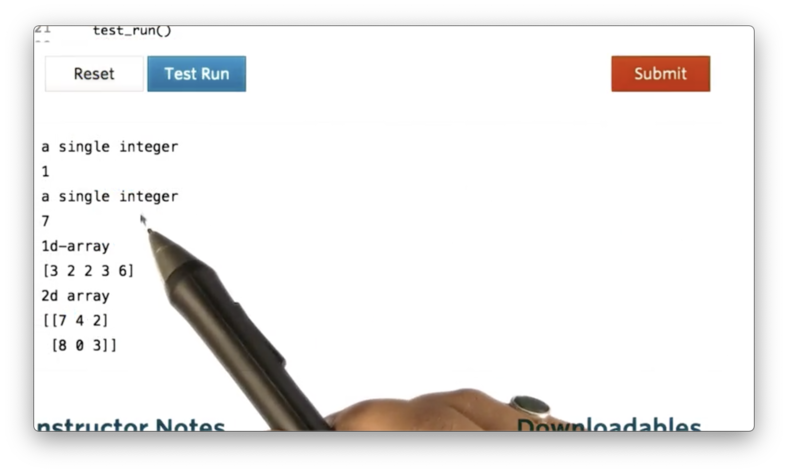
We can generate random integers using the `randint` method, like so:

```python
np.random.randint(10) # single integer in [0, 10)
np.random.randint(0, 10) # single integer in [0, 10)
```

Additionally, we can generate an ndarray of random integers with the `randint` method:

```python
# 5 random integers from [0, 10) in 1D ndarray
np.random.randint(0, 10, size=5)

# 2x3 array of random integers from [0, 10) 
np.random.randint(0, 10, size=(2, 3))
```

If we print the previous four examples, we see the following.

![](https://assets.omscs.io/notes/BFB422D8-4C0E-4D71-8F89-4E756F148793.png)

### Documentation

* [Random sampling](https://docs.scipy.org/doc/numpy-1.14.0/reference/routines.random.html)
* [numpy.random.random](https://docs.scipy.org/doc/numpy-1.14.0/reference/generated/numpy.random.random.html#numpy.random.random)
* [numpy.random.rand](https://docs.scipy.org/doc/numpy-1.14.0/reference/generated/numpy.random.rand.html#numpy.random.rand)
* [numpy.random.randint](https://docs.scipy.org/doc/numpy-1.14.0/reference/generated/numpy.random.randint.html#numpy.random.randint)

## Array Attributes

Any NumPy ndarray has several attributes that describe it, in addition to the elements it contains.

One of the most useful attributes is `shape`, which is essentially a tuple containing the number of rows and columns in the array. Let's create an array and access its shape:

```python
a = np.random.random((5,4))
a.shape
```

If we print out `a` and `a.shape`, we see the following.

![](https://assets.omscs.io/notes/DB3F6598-09CE-4A56-A8EB-A3189DE9DD87.png)

Since the shape is a Python tuple, which supports zero-based indexing, we can access just the number of rows or columns in `a` by indexing into the shape:

```python
a.shape[0] # rows
a.shape[1] # columns
```

We can determine the number of dimensions of an ndarray `nd` by passing the shape tuple to the builtin `len` function:

```python
len(nd.shape)
```

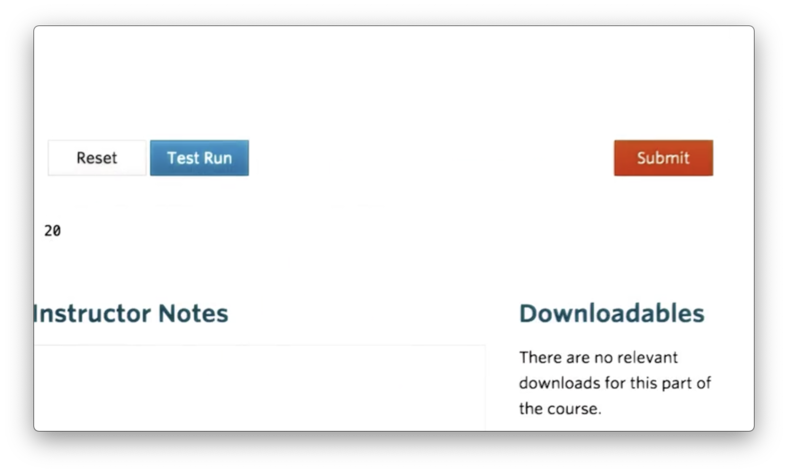
We can retrieve the number of elements present in an ndarray using the `size` attribute. For example, we can retrieve the size of `a`:

```python
a.size
```

If we print the size, we see the product of five rows and four columns.

![](https://assets.omscs.io/notes/FA013BE1-625B-4A7B-8A1A-2A0EA4AE23E3.png)

Attributes like size and shape are useful when you need to iterate over the elements in an ndarray to perform some computation.

Finally, you can access the data type of each element using the `dtype` attribute of the ndarray. For example:

```python
a.dtype
```

If we print the dtype of `a`, we see the following.

![](https://assets.omscs.io/notes/8A6A2B68-72B1-460A-B9D4-5DDE5C59F3F9.png)

We can see that the elements of `a` are all 64-bit floating-point numbers.

### Documentation

* [numpy.ndarray.shape](https://docs.scipy.org/doc/numpy/reference/generated/numpy.ndarray.shape.html)
* [numpy.ndarray.size](https://docs.scipy.org/doc/numpy/reference/generated/numpy.ndarray.size.html)
* [numpy.ndarray.dtype](https://docs.scipy.org/doc/numpy/reference/generated/numpy.ndarray.dtype.html)

## Operations on Ndarrays

Now let's look at performing various mathematical operations on ndarrays. Let's start by creating an array `a` with five rows and four columns, whose elements are random integers in `[0, 10)`:

```python
a = np.random.randint(0, 10, size=(5,4))
```

If we print `a`, we see the following.

![](https://assets.omscs.io/notes/ABB8CBB0-68CB-4A99-A6BD-24222E9C9819.png)

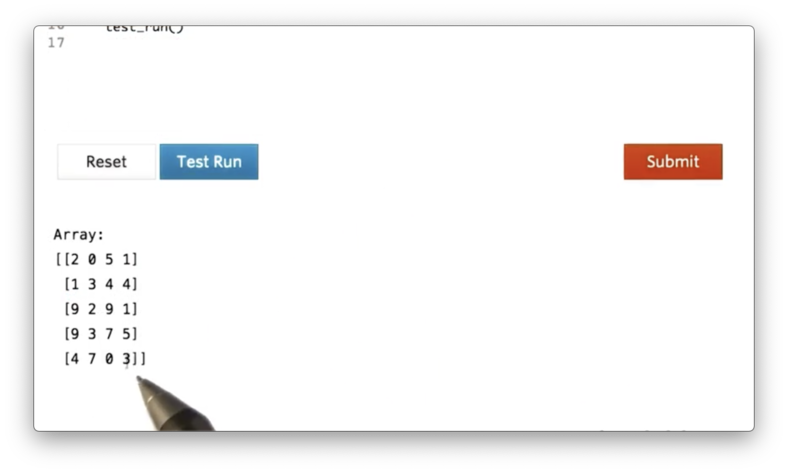
Summing all of the elements in `a` is as simple as calling the `sum` method of `a`:

```python
a.sum()
```

If we print `a` with `a.sum()`, we see the following.

![](https://assets.omscs.io/notes/817D6099-BFFA-49E3-9722-FCEC111A4790.png)

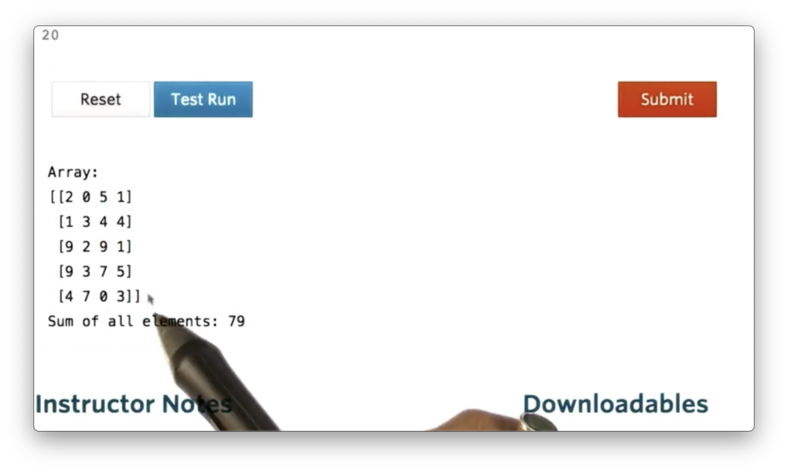
We can also calculate the sum of `a` in a specific direction. In other words, we can specify that we want to sum across the rows or down the columns of `a`.

We refer to this "direction" as an *axis*. The rows of an ndarray are aligned along axis zero, and the columns of an ndarray are aligned along axis one. Thus, if we want to sum all of the rows, we must sum along axis one, and if we want to sum all of the columns, we must sum down axis zero:

```python
a.sum(axis=0) # Sum columns
a.sum(axis=1) # Sum row
```

If we print these sums, we see the following.

![](https://assets.omscs.io/notes/7317FDBC-2E43-47DA-AE00-0F90638DC338.png)

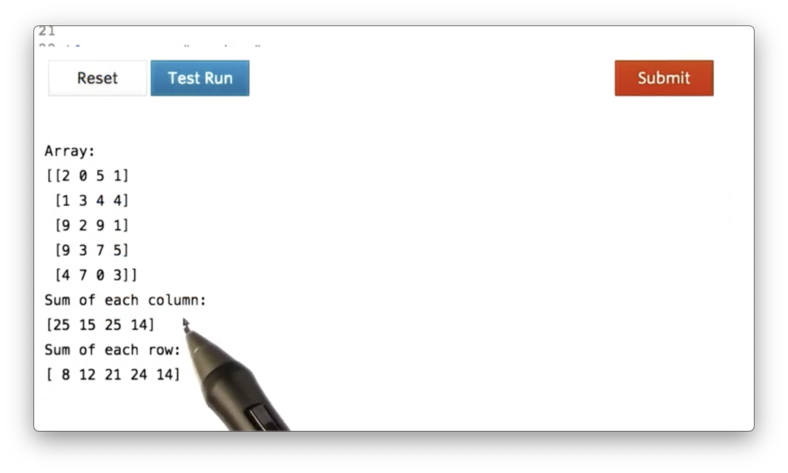
We can pull some basic statistics from an ndarray with the `min`, `max`, and `mean` methods, which all optionally take an `axis` parameter. for example:

```python
a.min(axis=0) # column minimum
a.max(axis=1) # row maximum
a.mean() # mean of all elements
```

If we print out these values, we see the following.

![](https://assets.omscs.io/notes/C4608A21-9B38-4FD8-A706-514F0CD1C643.png)

### Documentation

* [numpy.sum](https://docs.scipy.org/doc/numpy/reference/generated/numpy.sum.html#numpy.sum)
* [numpy.ndarray.min](https://docs.scipy.org/doc/numpy/reference/generated/numpy.ndarray.min.html)
* [numpy.ndarray.max](https://docs.scipy.org/doc/numpy/reference/generated/numpy.ndarray.max.html)
* [numpy.mean](https://docs.scipy.org/doc/numpy/reference/generated/numpy.mean.html#numpy.mean)

## Locate Maximum Value Quiz

![](https://assets.omscs.io/notes/55FC058B-8B31-4172-8F44-B44502611542.png)

Our task is to implement the function `get_max_index`, which takes a one-dimensional ndarray `a` and returns the index of the maximum value.

## Locate Maximum Value Quiz Solution

![](https://assets.omscs.io/notes/480BE86C-66FF-452B-965F-AD9833D98574.png)

We can retrieve the index of the maximum value in `a` with the `argmax` method:

```python
def get_max_index(a):
    return a.argmax()
```

### Documentation

* [numpy.argmax](https://docs.scipy.org/doc/numpy/reference/generated/numpy.argmax.html#numpy.argmax)

## Timing Python Operations

We claimed that NumPy is very fast, and we'd like to confirm this claim. To do so, we first need to understand how to time functions in general.

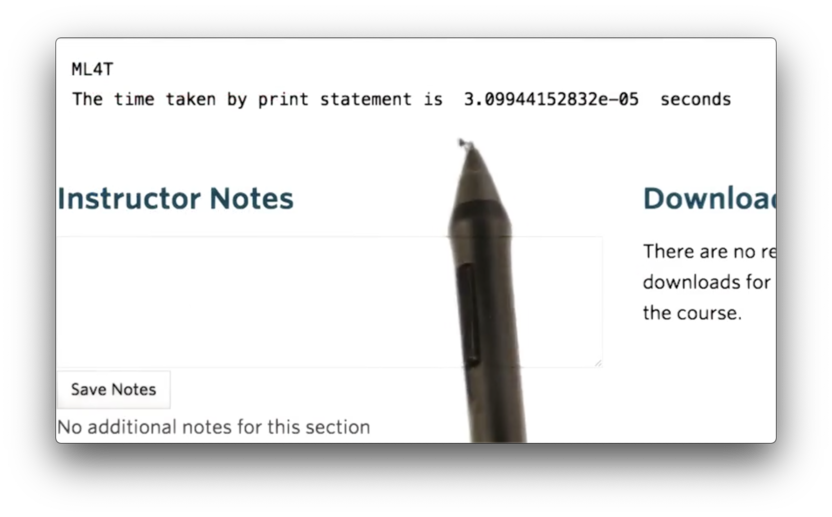
We can use the `time` module and the `time` function in that library to capture the current time. We compute the time before and after executing a function and take the difference to figure out how long a function took to execute.

```python
import time

t1 = time.time()
print "ML4T"
t2 = time.time()

print "The time taken by print statement is ", t2 - t1 ," seconds"
```

If we run this code, we see the following.

![](https://assets.omscs.io/notes/5C87242F-82A9-410D-8FAB-06EEDAC2A30C.png)

### Documentation

* [time](https://docs.python.org/3/library/time.html)
* [time.time](https://docs.python.org/3/library/time.html#time.time)

## How Fast is NumPy?

Now that we know how to time an operation in Python, let's check how fast NumPy is relative to naive Python code. We start by defining a really large array, `nd1`:

```python
nd1 = np.random.random((1000, 10000))
```

We want this array to be large enough so that the differences between execution durations become unmistakably significant.

We then define the two functions that we want to test. The function `numpy_mean` simply calls the `mean` method on the passed in `arr`. The function `manual_mean` iterates over all of the elements, sums them and then divides them by the total number of elements.

![](https://assets.omscs.io/notes/C38100EC-0430-4074-89D6-D6A1D8F682D2.png)

Finally, we define a `how_long` function, which itself receives a function `func` and some arguments `args`. The function times the execution of `func(*args)`, and then returns the result along with the duration.

![](https://assets.omscs.io/notes/70BCD191-CE9F-4886-82AF-F67CA83CD58C.png)

Let's check the difference in execution times.

![](https://assets.omscs.io/notes/DAE46E02-6B18-4E82-BA59-755CE5BCD910.png)

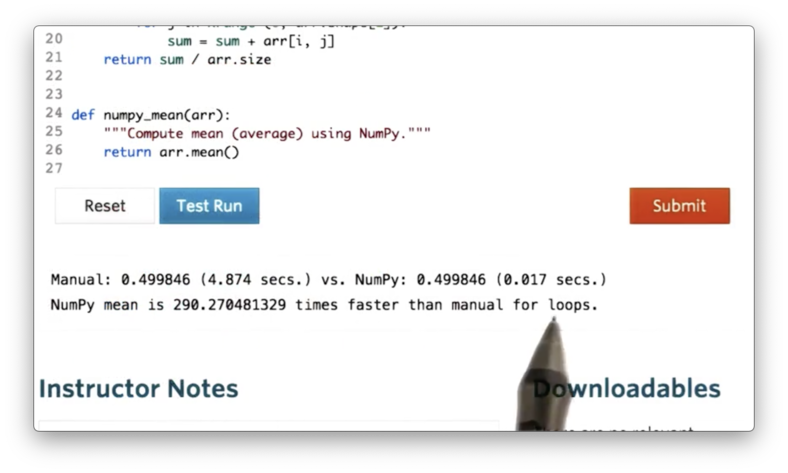
NumPy is close to 300 times faster than the simple iterative method!

## Accessing Array Elements

Accessing ndarray elements is straightforward. You can access a particular element by referring to its row and column number inside square brackets. For example, we can access the element in the fourth row and third column of `a` like so:

```python
a[3,2]
```

If we print out this value, we see the following.

![](https://assets.omscs.io/notes/C04548B7-4979-4580-997B-3445FDBC0CBF.png)

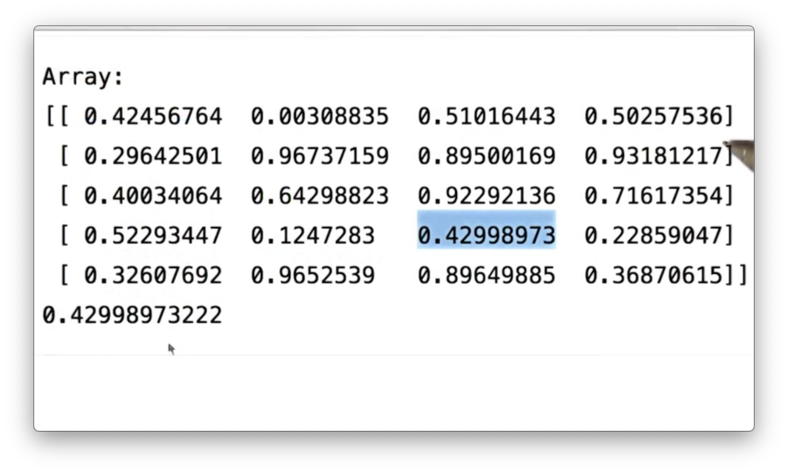
Additionally, we can access ranges of elements down columns and across rows using slicing. For instance, we can access the elements in the second and third columns of the first row of `a` like so:

```python
a[0, 1:3]
```

If we print this slice, we see the following.

![](https://assets.omscs.io/notes/DF27096A-2FBC-4359-ACD1-6C9074E7D243.png)

We can combine row and column slicing to select, for example, the elements in the first two rows and first two columns of `a` like so:

```python
a[0:2, 0:2]
```

If we print this slice, we see the following.

![](https://assets.omscs.io/notes/52A25CBB-C3BC-4ABA-96AB-80047042E742.png)

So far, we have only seen slice syntax like `x:y`, which defines a slice starting at row/column `x` and ending at row/column `y - 1`. We can specify a third parameter, `z`, which defines the *step size*.

For example, we can select all rows, but only the first and third columns of `a` like this:

```python
a[:, 0:3:2]
```

If we print this slice, we see the following.

![](https://assets.omscs.io/notes/89F330F0-8D5B-4889-A930-6229D47EC97B.png)

### Documentation

* [Indexing](https://docs.scipy.org/doc/numpy/user/basics.indexing.html)

## Modifying Array Elements

As well as accessing elements in ndarrays, we can also assign values to specific locations in ndarrays. As a simple example, we can set the first element in `a` to 1 like this:

```python
a[0, 0] = 1
```

Let's look at `a` before and after the assignment.

![](https://assets.omscs.io/notes/4155E98C-A86E-4850-9537-9DC8B691AA67.png)

We can use slicing for assignment as well as access. For example, we can set all of the elements in the first row of `a` like this:

```python
a[0, :] = 2
```

If we print `a`, we see the following.

![](https://assets.omscs.io/notes/F9E2FC3A-308E-4DFB-AE68-6ECA2C676103.png)

We don't have to set all of the elements in a row or column to the same value. If we assign a column or row to a list, each element will be set to the corresponding value in the list.

For example, we can set the fourth column of `a` to the values 1 through 5 with the following assignment:

```python
a[:, 3] = [1, 2, 3, 4, 5]
```

If we print `a`, we see the following.

![](https://assets.omscs.io/notes/9834AF37-F3E9-4E27-907E-B3C8ECC71576.png)

### Documentation

* [Indexing](https://docs.scipy.org/doc/numpy/user/basics.indexing.html)

## Indexing an Array with Another Array

An ndarray can also be indexed with another ndarray. To demonstrate this, let's first create an ndarray `a`:

```python
a = np.random.rand(5)
```

Next, let's create an ndarray `indices` whose elements represent the indices of the values we want to retrieve from `a`:

```python
indices = np.array([1, 1, 2, 3])
```

We can retrieve the values in `a` at the indices in `indices` like so:

```python
a[indices]
```

This expression is saying the following: for each element in `indices` retrieve the element in `a` at that index.

![](https://assets.omscs.io/notes/3851E9A3-E769-4AD1-8ED1-0077D88D704A.png)

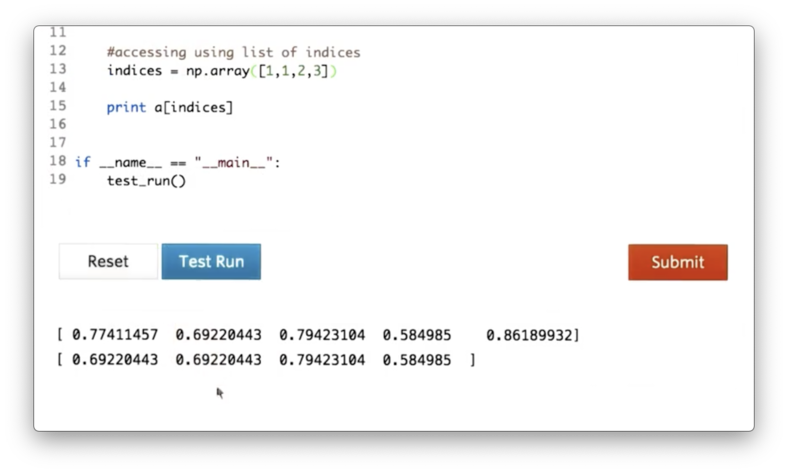
Indeed, we can see that our resulting array contains the elements of `a` at indices 1, 1, 2, and 3.

### Documentation

* [Indexing](https://docs.scipy.org/doc/numpy/user/basics.indexing.html)

## Boolean or "Mask" Index Arrays

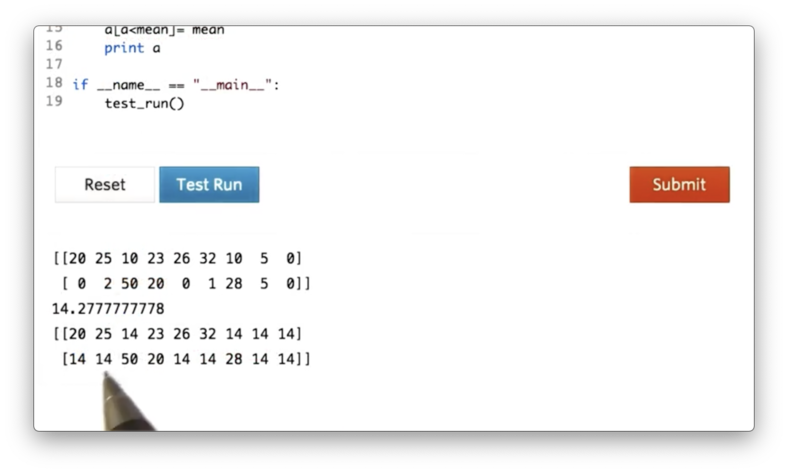
Let's see how we can retrieve all of the values from an ndarray that are less than the mean of that array. First, we construct our two-dimensional ndarray `a` and calculate the mean:

```python
a = np.array([
    (20, 25, 10, 23, 26, 32, 10, 5, 0)
    (0, 2, 50, 20, 0, 1, 28, 5, 0)
])

mean = a.mean()
```

If we print `a` and `mean`, we see the following.

![](https://assets.omscs.io/notes/DCB7B910-7F1E-4003-8921-BD8E9600887E.png)

While we can technically run a `for` loop over the elements in `a` and keep only those values less than 14.2, there is a cleaner way:

```python
a[a < mean]
```

We can interpret this expression as: for each value `a_i` in `a`, compare `a_i` with `mean` and retain the value if `a_i > mean`.

If we print the output of the expression, we see the following ndarray.

![](https://assets.omscs.io/notes/4AAD096B-B54B-4471-8BD6-5A1E542DC5BA.png)

Additionally, we can use this masking technique to set the values of `a` that are less than `mean` to `mean`:

```python
a[a < mean] = mean
```

If we print `a` now, we see the following.

![](https://assets.omscs.io/notes/55ECA174-CE17-4395-A26E-4775193C04BF.png)

### Documentation

* [Indexing](https://docs.scipy.org/doc/numpy/user/basics.indexing.html)

## Arithmetic Operations

Arithmetic operations on ndarrays are always applied element-wise. Let's first create an ndarray `a`:

```python
a = np.array([
    (1, 2, 3, 4, 5), 
    (10, 20, 30, 40, 50)
])
```

We can multiply each element in `a` by two:

```python
2 * a
```

If we print the result of this multiplication, we see the following.

![](https://assets.omscs.io/notes/398DF573-0F38-4286-9EDD-C9232C7686FE.png)

We can divide each element in `a` by two:

```python
a / 2
```

If we print the result of this division, we see the following.

![](https://assets.omscs.io/notes/9F151FEC-7765-4C2F-A3FB-153AA51653CF.png)

Note that both the divisor and the elements in the ndarray are integers. As a result, integer division (rounding down, roughly) is performed, which is why 1 / 2 equals 0.

We can cast the resulting array into float values by ensuring that the divisor is a float:

```python
a / 2.0
```

If we print the result of this division, we see the following.

![](https://assets.omscs.io/notes/1A8906A1-E16C-43DF-9871-15CA746AA16A.png)

Our arithmetic capabilities are not limited to just operations between ndarrays and scalar values. We can also perform operations that combine two ndarrays. Let's create a second ndarray `b`.

```python
a = np.array([
    (100, 200, 300, 400, 500), 
    (1, 2, 3, 4, 5)
])
```

We can add `a` and `b`:

```python
a + b
```

If we print the result of this addition, we see the following.

![](https://assets.omscs.io/notes/E73AD763-5D55-48FA-9F93-C7561BBC9F43.png)

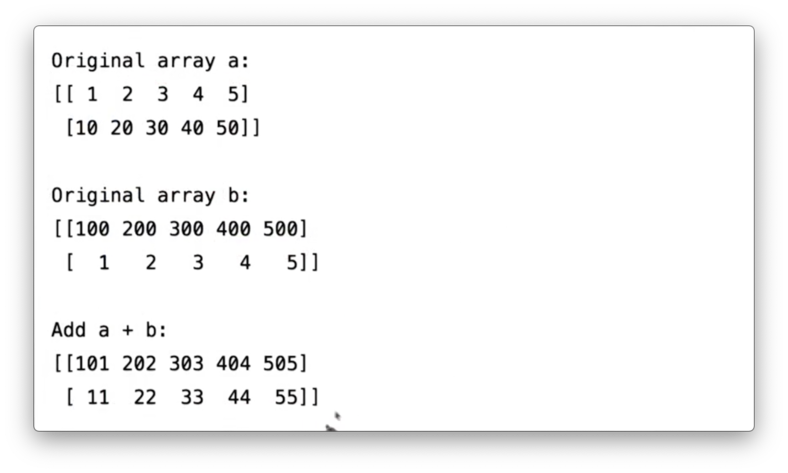
Note that the shape of `a` and `b` should be similar before trying to perform operations that involve both ndarrays; otherwise, NumPy will throw an error.

The multiplication operator allows us to multiply two ndarrays in an element-wise manner. Note that other languages commonly use the multiplication operator to signify the dot product. NumPy does *not* do this.

We can multiply `a` and `b` in an element-wise fashion:

```python
a * b
```

If we print the result of this multiplication, we see the following.

![](https://assets.omscs.io/notes/8B333BFA-719A-4D1F-A85E-26F56AD29E64.png)

We can divide `a` by `b`:

```python
a / b
```

If we print the result of this division, we see the following. Remember that we are doing integer division here.

![](https://assets.omscs.io/notes/A2A00FC6-4BA6-4DD8-B46F-3770DDBA7BDA.png)


---

# Agent Instructions: Querying This Documentation

If you need additional information that is not directly available in this page, you can query the documentation dynamically by asking a question.

Perform an HTTP GET request on the current page URL with the `ask` query parameter:

```
GET https://matthewcaseres.gitbook.io/scs/machine-learning-trading/power-of-numpy.md?ask=<question>
```

The question should be specific, self-contained, and written in natural language.
The response will contain a direct answer to the question and relevant excerpts and sources from the documentation.

Use this mechanism when the answer is not explicitly present in the current page, you need clarification or additional context, or you want to retrieve related documentation sections.